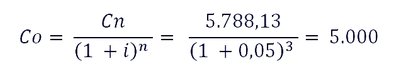En toda operación financiera se debe buscar el equilibrio entre los cobros y los pagos cuando estos se dan en períodos diferentes del tiempo. Es lo que se denomina  Equivalencia financiera:

Diferentes sumas de dinero en tiempos

diferentes pueden tener el mismo valor 

Entre la entrega y la devolución de un capital debe existir una equivalencia referida a un momento determinado. De hecho, la equivalencia financiera lo que intenta es calcular el tipo de interés que hace que dos capitales distintos, situados en diferentes momentos, sean equivalentes.

También nos puede servir para  saber qué operación financiera es más interesante desde el punto de vista financiero.

Así, si tenemos varios capitales de diferentes cuantías y situados en diferentes momentos de tiempo puede resultar conveniente compararlas para ver cuál es mejor. Pero esta comparación deber ser homogénea, es decir, tendríamos que llevar todos los capitales a un mismo momento del tiempo y ahí efectuar la comparación.

Para realizar esta homogeneización (igualar estos capitales en un momento determinado) se utilizan las Leyes financieras de Capitalización y Actualización.

¿Cuánto vale mañana un euro de hoy?   ¿Cuánto tendré dentro de 3 años si invierto hoy 5.000 € al 5%?

Éstas son las preguntas a las que responde la Capitalización. Cuando proyectamos un  capital a un momento posterior en el tiempo a su origen, se dice que estamos aplicando una ley financiera de Capitalización.

Capitalizar es calcular el valor de un  capital financiero equivalente de un capital presente en un momento futuro. Es  llevar un capital a un momento en el futuro. Es calcular el valor final de un valor inicial.

Hablando claro: Capitalización es cuando se lleva cierta suma de dinero “hacia adelante” (ver gráfico 1) y se utiliza para saber cuánto vale un euro de hoy dentro de un mes, de un año, etc.

Ejemplo:

- HOY: Tenemos 5.000 € (Capital inicial) que invertimos al 5% para que nos genere una renta durante 3 años.

- Al final de estos 3 años: Tendremos 5.788,13 € (Capital final =  Capital inicial  + intereses).

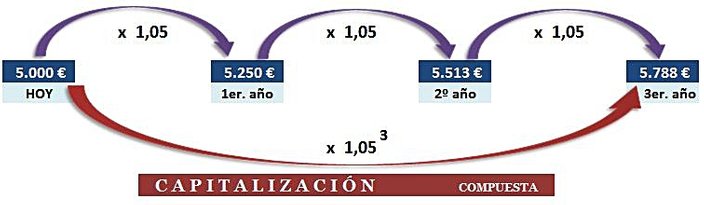
GRÁFICO 1

El proceso descrito en la gráfica anterior (capitalización compuesta) consiste en calcular un capital futuro (5.788,13 €) equivalente a un capital presente (5.000 €):

- Al final del 1er.  año tendremos los 5.000 iniciales más 5.000 x 0,05  de intereses = 5.250

- es decir:   5.000 x 1,05

- Al final del 2º año, los 5.250 anteriores más 5.250 x 0,05  de intereses =  5.5130

- es decir:   5.250 x 0,05   =   5.000 x 1,05 x 1,05   =   5.000 x (1,05)²

- Al final del 3er.  año, los 5.512,50 más 5.512,50 x 0,05  de intereses =  5.788,13

- es decir:   5.512,50 x 0,05   =   5.000 x 1,05 x 1,05 x 1,05   =   5.000 x (1,05)³

En resumen: En la capitalización un capital presente, denominado capital inicial, se sustituye por otro capital futuro, denominado capital final.

¿Cuánto vale  hoy un euro de mañana? ¿Cuánto tengo que invertir hoy al 5% para obtener  dentro de 3 años 5.788 €?

Éstas son las preguntas a las que responde la Actualización.  Se trata de la operación inversa a la Capitalización. Llevar un capital final a un momento del tiempo anterior, recibe el nombre de Actualización o Descuento.

Actualizar es calcular la cuantía de un capital financiero equivalente de un capital futuro en el presente.  Es traer un capital al presente. Es calcular el valor inicial de un valor final.

Actualización es cuando se trae cierta suma de dinero "hacia atrás" (ver gráfico 2) y se utiliza para saber cuánto vale hoy un euro del mes que viene, del año que viene,  etc.

Como hemos dicho, se trata de la operación inversa a la capitalización. Siguiendo con el mismo ejemplo:

Ejemplo: ¿Qué cantidad deberíamos depositar hoy para obtener 5.788,13 € dentro de 3 años si nos están ofreciendo un 5% de interés?

- Dentro de  3 años nos entregarán 5.788,13 € (Capital final) por haber invertido hoy una cantidad al 5% de interés.

- HOY: esta cantidad inicial equivalente sería 5.000 € (Capital inicial).

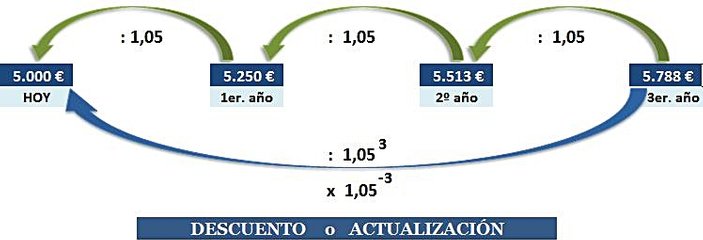
GRÁFICO 2

El proceso descrito en la gráfica anterior (actualización compuesta) consiste en  calcular un capital actual (5.000 € ) equivalente a un capital futuro (5.788,13 €):

- Al final del 2º año tendremos los 5.788,13 del año 3 menos los intereses que hubiera generado el capital del año 2: 5.788,13 - 275,63 = 5.512,50

- es decir: 5.788,13 / 1,05

- Al final del año 1, los 5.512,50 del año 2 menos los intereses que hubiera generado el capital del año 1: 5.512,50 - 262,50 = 5.250

- es decir: 5.250 / 1,05   =   5.788,13 / 1,05 / 1,05 = 5.788,13 / (1,05) ²

- Al principio del año 1, los 5.250 del final del año 1 menos  que hubiera generado el capital inicial de principios del año 1;

- es decir: 5.250 / 1,05   =   5.788,13 /1,05 / 1,05 / 1,05 = 5.788,13 / (1,05) ³

En resumen:

En la actualización un capital futuro, denominado capital final, se sustituye

por otro capital presente, denominado capital inicial o valor actual.

Hemos "llevado" una cantidad de hoy (con su valor actual) hasta un período de 3 años, con su valor final (CAPITALIZAR).

Lo contrario, es decir, "traer" al presente una cantidad futura se denomina Actualizar y para calcularla se realiza la operación inversa a la capitalización:

en lugar de multiplicar por      (1+i)ⁿ  se divide por (1+i)ⁿ   

O lo que es lo mismo, se multiplica por    1/(1+i)ⁿ   

que es lo mismo  que multiplicar por              (1+i)-ⁿ

^{En   ACTUALIZACIÓN (o DESCUENTO)}

^{Para pasar una cantidad de un año al anterior} 

se divide por (1+i)ⁿ    o se multiplica  por    (1+i)-ⁿ 

Asimismo, podemos calcular el Capital Inicial C₀ dividiendo el Capital Final C_n por el coeficiente (1+i) ⁿ, donde i es el tipo de interés  y n el número de años: